В окружающем мире есть много примеров повторяющихся процессов и движения: например - движение качелей или маятниковых часов,вращение тела по окружности, морские приливы и отливы и т. д.. Если значения физических величин, которые характеризуют такие процессы и движения, повторяются через равные промежутки времени, то эти процессы и движения нвзываются периодическими.

Одной из важных характеристик периодического процесса и движения является период (Т) - время одного полного повторения. Период измеряется в секундах (с). Если рассмотреть равномерное движение точки по окружности, то это будет повторяющееся движение для наблюдателя, который смотрит на это движение прямо. А для наблюдателя, который смотрит на это движение со стороны, такое движение будет восприниматься как возвратное движение по прямой линии, между точками А и В (смотри рисунок)

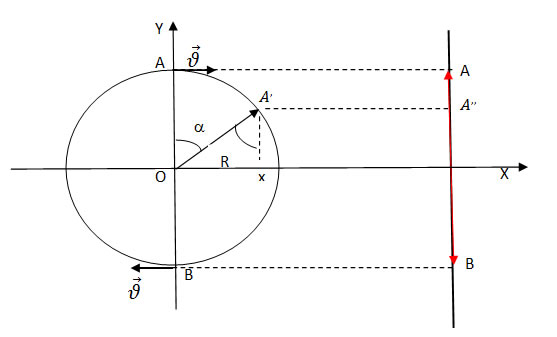
Здесь можно увидеть два вида движения: повторяющееся движение по окружности по пути АВА и повторяющееся возвратное движение "тени"по прямой между точками АBВА (красный отрезок). Когда точка А проходит путь АА^,, совершая угловое перемещение , то проекция этой точки по оси ОХ совершает перемещение ох, а по оси ОУ - перемещение AA^,,.

Повторяющееся движение "тени" и вдоль оси ОХ и вдоль оси ОУ, обладающее свойством возвратности называется колебательным движением.

Таким образом подведём итог: при определённых условиях двухмерное движение по окружности может восприниматься как одномерное колебательное движение.

Ещё раз вернёмся к рисунку. Пусть тело начинает движение из т.А. Тогда в любой момент времени его координаты х и у можно определить из треугольника ОА^,х:

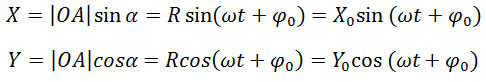
В этих уравнениях - это угол поворота радиуса, соединяющего т.О (центр окружности) с точкой, в которой находится тело, т.А. Эту величину называют фазой колебаний и часто обозначают буквой . Эту величину также называют угловым перемещением, которое можно найти как

= = . Где - угловая скорость. По определению (смотри движение по окружности) углрвая скорость - это число оборотов за 2n cекунды (за 6,28 с) и её можно вычислить по следующим формулам

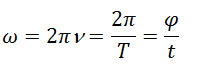
Угловое перемещение можно определить математически: в радианах оно равно отношению дуги окружности (путь, который пройдёт тело) к радиусу окружности R, а радиус окружности в свою очередь равен максимальному отклонению от точки равновесия Х₀ или У₀ :. Величинуназывают начальной фазой.

Период колебаний можно определить по формуле .

Величина - частота колебаний. Частота колебаний и циклическая частота измеряются в Гц или 1/с.

Рассмотрим колебательное движение вдоль оси ОХ:

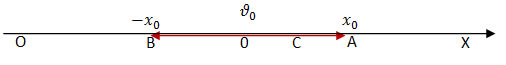
Колебания совершает тело между точками А и В.

Если колебания начинаются из точки 0, то в начальный мрмент времени (t=0) координата Х = 0, значит функция, с помощью которой описывается такое колебание это sin, т.е. колебания будут синусоидальными

.

Через время, равное четверти периода (t = T/4) тело окажется в т.A, координата будет равна

.

Через время, равное половине периода (t = T/2) тело снова окажется в т.О, координата будет равна

.

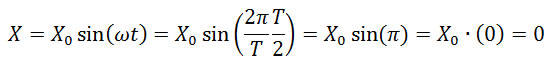
Через время, равное трём четвертям периода (t = 3T/4) тело окажется в т.B, координата будет равна

.

Через время, равное периоду (t = T) тело окажется в т.О, т.е. вернётся в первоначальное положение, координата будет Х = 0.

Если колебания начинаются из точки A, то в начальный мрмент времени (t=0) координата Х = X₀ - амплитуде (максимальному значению) координаты значит функция, с помощью которой описывается такое колебание это cos, т.е. колебания будут косинусоидальными

.

Через время, равное четверти периода (t = T/4) тело окажется в т.О, координата будет равна

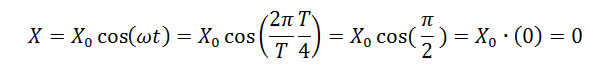
Через время, равное половине периода (t = T/2) тело окажется в т.В, координата будет равна

.

Через время, равное трём четвертям периода (t = 3T/4) тело окажется в т.A, координата будет равна

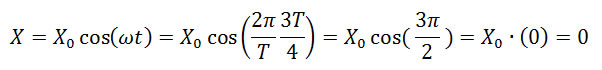
Через время, равное периоду (t = T) тело вернётся в первоначальное положение и окажется в т.A, координата будет равна Х = X₀.

Если какой либо параметр физической системы (тела) изменяется с течением времени, совершая гармонические колебания с некоторой частотой, то такие же колебания ( с такой же частотой) будут совершать так же скорость и ускорение, с которыми меняется данный параметр.

Мы рассмотрели колебательное движение тела вдоль оси ОХ и определили расчётные формулы координаты данного движения. Если координата будет изменятся с течением времени, то с такой же частотой будут изменяться скорость и ускорение тела.

Из определения, скорость есть изменение координаты в единицу времени или первая производная от координаты: .

Ускорение есть изменение скорости в единицу времени или первая производная от скорости , или вторая производная от координаты а = х^,,.

В формулах это будет выглядеть так:

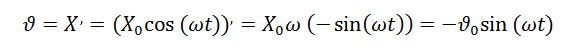
или,

где - амплитуда (максимальное значение) скорости колебаний.

,

где - амплитуда (максимальное значение) ускорения колебаний. Если тело совершает колебания со скоростью колебаний, то оно обладает кинетической энергией колебаний - значение кинетической энергии в любой точке траектории колебательного движения разное, в т. А и т.В К = 0Дж.

В точке О кинетическая энергия колеблющего тела принимает максимальное значение .

Полная энергия колебательного движения в любой точке, в любой момент времени

равна сумме кинетической и потенциальной энергии тела W = K_max= П_max= К + П.

Если есть ускорение колебания, значит была причина (сила колебаний), вызвавшая это ускоренное движение. Согласно 2 закону Ньютона: F = ma.

Любое механическое клебательное движение можно описать с помощью моделей: математического маятника, пружинного маятника и конического маятника.

Вернуться к конспектам урока