Математическим маятником (ММ) называется находящееся в поле тяжести, подвешенное на тонкой нерастяжимой нити тело, размеры которого малы по сравнению с длиной нити, а масса значительно больше массы нити. Такое тело можно считать точечным (материальной точкой), а нить - невесомой. ММ - это модель, с помощью которой можно полностью охарактеризовать колебательное движение, возникающее под действием силы тяжести тела и силы натяжения нити.

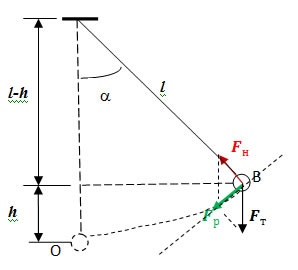
Когда тело висит вертикально, то результирующие всех сил (F_р), действующих как на тело так и на нить, равны нулю, и система находится в равновесии. Если тело отвести от положения равновесия на угол и отпустить без начальной скорости, то тело начинает совершать малые колебания относительно положения равновесия, которые будут происходить в вертикальной плоскости.

Использую второй закон Ньютона получим:.

Запишем данный закон в проекции на оси координат

ОХ:;

ОУ:.

Решая это уравнение, выражая силу натяжения из первого уравнения и подставляя её во второе уравнение получим ,

где. Из рисунка видно что .

Если угол отклонения маятника от вертикали мал, тои

, h = 0 . В этом случае можно считать что маятник совершает колебания только вдоль ост ОХ, а значит, т.е. а_y = 0 можно принять равным нулю. Тогда уравнение для определения ускорения примет вид. Подставляя значения ускорения и скорости в это уравнение, получим - период колебания ММ;

- частота колебаний ММ; - циклическая частота колебаний ММ.

Из формул видно что частота и период колебаний ММ не зависят от массы тела. Полная энергия колебаний математического маятника есть величина постоянная:

W - полная энергия системы, П_max = mgh_max - максимальная потенциальная энергия,

- максимальная кинетическая энергия.

Если ММ движется с ускорением a вниз (или вверх, но с замедлением), то период его колебаний будет определяться выражением.

Если ММ движется с ускорением a вверх (или вниз, но с замедлением), то период его колебаний будет определяться выражением.

Если ММ движется с ускорением a горизонтально ( т.е. перпендикулярно ускорению свободного падения g), то период его колебаний будет определяться выражением

.

Если ММ поднять на высоту h, сравнимую с радиусом Земли R = 6,4*10⁶ м, то ускорение свободного падения g на этой высоте будет меньше ускорения свободного падения на поверхности Земли и рассчитать его можно по формуле

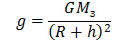
Здесь G = 6,67*10^-11 Hм² /кг² - гравитационная постоянная. М_з =6*10²⁴ кг.

Вследствие уменьшения ускорения свободного падения на высоте h период свободных незатухающих колебаний ММ станет больше периода на Земле на величину . При этом справедливо соотношение, где t - время работы маятника, а - время отставания ММ.

Если ММ несет на себе заряд и колеблется в однородном электрическом поле с напряжённостью Е, то на него будет действовать сила Кулона F_кл = qE, которая сообщает маятнику дополнительное ускорение F_кл = ma.

Если маятник проедставляет собой стержень, колеблющийся в однородном магнитном поле индукцией В со скоростью v, то в этом стержне будет действовать ЭДС электромагнитной индукции, вследствие чего на концах стержня возникает разность потенциалов U = Bvlsina. Где а - угол между вектором скорости стержня и вектором магнитной индукции магнитного поля.

Если маятник не является ни пружинным, ни математическим, ни коническим ( физический маятник), то его характеристики ( период, частоту, циклическую частоту) нельзя рассчитать по вышезаписвнным формулам. Эти характеристики можно найти из формулы силы, действующей на маятник, или из формулы полной энергии.

Пример: Тело цилиндрической формы высотой Н с площадью поперечного сечения S, изготовленное из материала плотностью , находится в жидкости плотностью , погрузившись наполовину, т.е. покоится, не всплывая и не опускаясь вниз с ускорением.

Решение: На тело действуют сила тяжести и сила Архимеда . Где V - объем тела, V = SH. V_погр = 0,5SH - объем погруженной части тела. Если тело погрузить на глубину h, то оно начнёт колебаться за счёт того что новая си ла Архимеда превысит силу тяжести. Тогда по второму закону Ньютона

, где

и .

Решая систему этих уравнений получим , отсюда . Вычислив циклическую частоту, можно рассчитать частоту и период колебаний.

Вернуться к конспектам урока