Вернёмся  к  основному  уравнению  движения:  $X = X_0 + \Delta r$, $X = X_0 + \vartheta \Delta t$
Т.к. тело  движется  неравномерно (с разными  скоростями), то  уместно  говорить  и  рассматривать среднюю  скорость  движения, тогда  в формуле  движения  вместо  скорости необходимо записывать  среднюю  скорость:
$X = X_0 + <\vartheta> \Delta t$
Когда скорость изменяется на одинаковую величину в единицу t, то такое движение называется равноускоренным (равноизменяющимся). При  этом среднюю  скорость  можно  вычислять  через  начальную  и  конечную  скорости (а  не  брать  все имеющиеся  её значения), т.е. вместо $<\vartheta>=\dfrac{\vartheta_1+\vartheta_2+\vartheta_3+...+\vartheta_N}{N}$, пользоваться  более короткой формулой: 

$<\vartheta>=\dfrac{\vartheta+\vartheta_0}{2}$
тогда формула $\Delta r = <\vartheta> \Delta t$ примет  вид:

$\Delta r = \dfrac{\vartheta+\vartheta_0}{2} \Delta t$

Изменение скорости в единицу времени называется  ускорением движения тела.
$\dfrac{\Delta \vartheta}{\Delta t}=\dfrac{\vartheta - \vartheta_0}{\Delta t}=a=\vartheta '$ (формула ускорения) по определению, ускорение  есть производная от  скорости  или вторая производная  от координаты.
$\Delta t = \dfrac{\vartheta - \vartheta_0}{a}$ (формула  времени, в течение  которого изменяется  скорость)
$\vartheta = \vartheta_0+a\Delta t$ - уравнение мгновенной скорости (скорость тела в любой точке траектории, в любой  момент  времени)
Если  значения  скорости  или  времени  подставить  в  формулу  перемещения,  то получим  несколько  формул  для  вычисления  перемещения  тела  при  равноускоренном  движении:
$\Delta r = \dfrac{\vartheta^2-\vartheta_0^2}{2a}$, $\Delta r = \vartheta_0 t + \dfrac{at^2}{2}$, если  вернуться  к  общей формуле  движения $X = X_0 + \Delta r$ , то  уравнение  равноускоренного движения  примет  вид
$X=X_0+\vartheta_0 t+\dfrac{at^2}{2}$ уравнение равноускоренного движения.
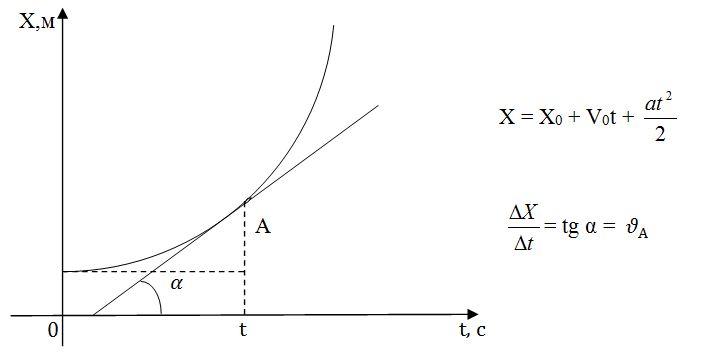
Графиком  такого  уравнения  будет  парабола (аналогия квадратного уравнения в математике)

 

 

 

$X=X_0+\vartheta_0 t+\dfrac{at^2}{2}$
$\dfrac{\Delta X}{\Delta t}=tg{\text{ }\alpha}=\vartheta_A$

 

 

 

Если  коэффициент при t, $a > 0$, то ветви параболы будут направлены вверх ↑ (разгон), если $a < 0$, то ветви параболы будут направлены вниз ↓(торможение).  
На данном  графике, как и на графике  при равномерном  движении  графический смысл скорости тот же: $\dfrac{\Delta X}{\Delta t}=tg{\text{ }\alpha}=\vartheta_A$. Отличие: здесь нужно  рассматривать  наклон  касательных  к  точкам  графика, тангенсы  углов  их  наклона  и  будут  значениями  скоростей  в  каждый  момент  времени (в  каждой  точке  траектории).
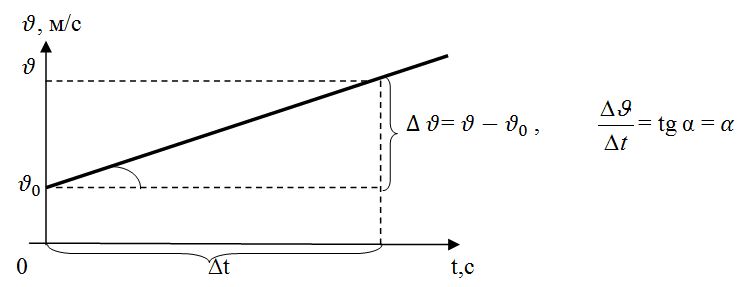
На  графике зависимости  скорости  от  времени:

Графический  смысл  перемещения  также  будет  площадь  фигуры  под  графиком, но это  уже  площадь  прямоугольной  трапеции, лежащей  на  боку, её  высотой  будет промежуток  времени, а  основаниями  значения  начальной  и конечной  скоростей:
$\Delta r = S = (\dfrac{a+b}{2}h)=\dfrac{\vartheta_0+\vartheta}{2}\Delta t$   
Графический  смысл  ускорения  на  этом  графике  -  тангенс  угла  наклона  графика  скорости  к  оси  времени:
$\dfrac{\Delta \vartheta}{\Delta t}=tg{ \text{ }\alpha} = a$ (тангенциальное  ускорение)
Если принять начальную скорость равную нулю, то все формулы  равноускоренного  движения упрощаются, т.е.
если $\vartheta_0 = 0$, то
$X=X_0+\dfrac{at^2}{2}; \Delta r = <\vartheta>t; \Delta r = \dfrac{\vartheta^2}{2a}; \Delta r = \dfrac{\vartheta}{2}t; \Delta r = \dfrac{at^2}{2}; \vartheta = at$.

Поставим перед собой цель определить перемещения  за  отдельные  промежутки времени, например, за каждую 1 секунду, при этом начальная скорость равна 0: 
за первую 1с,  вторую 1с, третью 1с   и    т.д.
Перемещение тела за  первую  1 секунду: $\Delta r_1 = \dfrac{at^2}{2} = \dfrac{a*1^2}{2} = \dfrac{a}{2}*1$
Перемещение за  вторую 1 секунду найдём как разность между перемещениями за две секунды и за одну  секунду: $\Delta r_2 = \dfrac{a(t_1+t_2)^2}{2} - \dfrac{at_1^2}{2} = \dfrac{a}{2}*3$, где $t_1$ и $t_2$ - это промежутки по 1с, а их сумма это 2 с и т.д.     
Таким образом, каждую одну секунду тело проходит путь (перемещение), которое кратно целому нечётному числу:

Пример: если тело начало движение (т.е. начальная скорость равна нулю) с ускорением $a = \text{4 м/с}^2$, то оно совершит перемещения
за первую 1с: - 2м ($\Delta r_1 = \dfrac{a}{2}*1$)
за вторую 1с: - 6м ($\Delta r_2 = \dfrac{a}{2}*3$), это перемещение больше предыдущего на величину равную а=4                                
за третью 1с: - 10 м ($\Delta r_3 = \dfrac{a}{2}*5$), это перемещение больше предыдущего на величину равную а=4
за четвертую 1с: - 14 м   ($\Delta r_4 = \dfrac{a}{2}*7$), это  перемещение  больше предыдущего  на величинуравную а=4,
за пятую 1с: - 18 м    ($\Delta r_5 = \dfrac{a}{2}*9$) и т.д.
общая  формула  для  определения  перемещения  за  n-ую   одну  секунду:

$\Delta r_n = \dfrac{a}{2}(2n-1)$ где  n - это  номер  одной  секунды  ( первой, второй, ....... десятой,......сотой)
Каждое  перемещение  отличается  на  величину  численно  равную  числовому  значению  ускорения.
Если  рассматривать  промежутки  времени  не за 1с, а за каждые 2с  ( первые  2с, вторые 2с,  третьи  2с   и  т.д.),  то промежутки  перемещений будут  зависеть  ещё  и от  квадрата  времени:
$\dfrac{at_1^2}{2}*1$ - перемещение за первые 2с,
$\dfrac{at_1^2}{2}*3$ - перемещение за вторые 2с,
$\dfrac{at_1^2}{2}*5$ - перемещение за третьи 2с,  и  т.д.
!!!  Тогда  общая  формула такого  движения $\Delta r_n = \dfrac{at^2}{2}(2n-1)$       
где  n - это номер одной (или t) секунды; t – время одного промежутка (первые 2с, вторые 2с,........, десятые 2с.....).

Вернуться к конспектам урока