Равномерное движение -  это движение,  при котором изменение координаты за единицу времени есть величина постоянная $\frac{\Delta X}{\Delta t} = const$, т.е. $\vartheta = const$, тогда $X = X_0 +\vartheta \Delta t$ – уравнение равномерного движения, где  $X$ - функция, а $t$ – аргумент, т.е. это изменение  координаты  в  зависимости  от  времени – Х(t).
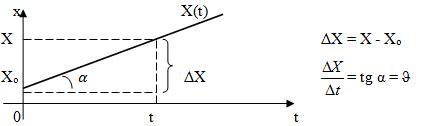
Графиком такой функции является прямая линия:

 

$\Delta X = X - X_0$
$\frac{\Delta X}{\Delta t} = tg{\alpha}=\vartheta$

графический смысл скорости: $\vartheta$ – это тангенс угла (α) наклона графика Х(t) к оси $t$ (оси абсцисс).
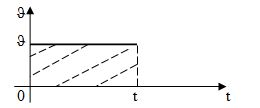
Т.к. скорость  величина  постоянная, то  графиком  зависимости скорости  от  времени $\vartheta(t)$ будет  прямая линия  параллельная  оси  времени (Ot):

Графический  смысл  перемещения  -  это площадь  фигуры  ограниченной  осями  координат, графиком  и перпендикулярами, опущенными на  ось  времени:
$\Delta r = \vartheta t = S$ площадь прямоугольника. Для прямолинейного движения модуль перемещения равен пути, поэтому при прямолинейном движении методы нахождения перемещения (графический и алгеброический) справедливы и для определения пути.

Вернуться к конспектам урока