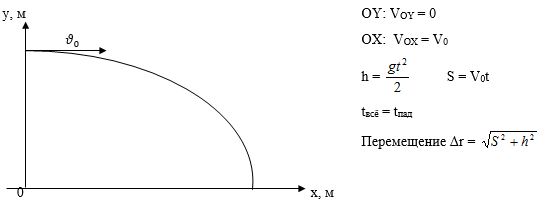
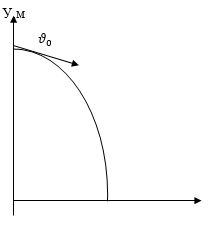
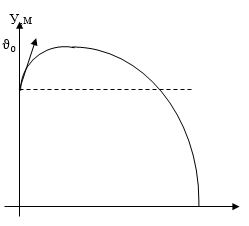
(Данное движение состоит из двух движений: Вертикальное равноускоренное   движение и Равномерное горизонтальное).
Какие   отличия можно отметить между данным движением и ранее рассматривающимися    РуВД и РмГД?
1 отличие: в том, что скорость при вертикальном движении, равна вертикальной составляющей  – $\vartheta_y$ (вертикальной  проекции), а  горизонтальное  движение  происходит  с  горизонтальной  составляющей  скорости - $\vartheta_x$.(Эти проекции скоростей выражаются через тригонометрические функции Sin и Cos).
2 отличие: в том, что свободное движение по вертикали протекает с ускорением свободного падения $g$, а при движении под углом к горизонту по оси ОУ движение может быть как свободным (с ускорением $g$), так и любым равноускоренным движением с ускорением $a_{т}$ .
3 отличие:в том, что перемещение тела происходит вверх-вниз (h) – высота подъёма и вперёд (S) – дальность полёта.
                   
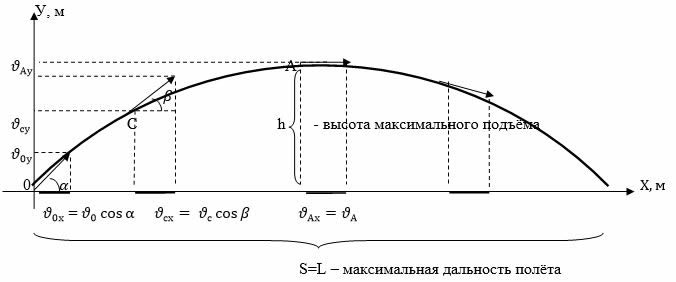
Рассмотрим свободное движение (только под действием силы тяжести) вдоль оси Oу - вертикальное:
OY: Определим   проекции   скоростей в точках О, С, А и сравним их по величине.
На рисунке хорошо видно, что проекции этих скоростей отличаются по величине: 
$\vartheta_{OY} > \vartheta_{CY} > \vartheta_{AY}$, при этом проекция скорости в точке А на ось OY равна нулю ($\vartheta_{AY}=0$), а  проекции  остальных  скоростей  соответственно:
$\vartheta_{OY}=\vartheta_O \sin \alpha$, $\vartheta_{CY}=\vartheta_C \sin \beta$.
По  определению  основных  характеристик  вертикального  движения можно  записать  их  формулы:       
1.Время подъёма тела на высоту h: $t_{под}=\dfrac{\vartheta_{AY}-\vartheta_{OY}}{g}=\dfrac{\vartheta_{OY}}{g}=\dfrac{\vartheta_0 \sin \alpha}{g}$
2.Конечная скорость подъёма в т.А:  $\vartheta_{AY} = \vartheta_{OY} - gt_{под}$, но т.к. $\vartheta_{AY} = 0$, то эту формулу можно записать в виде: $0 = \vartheta_0 sin~\alpha - gt_{под} \Rightarrow \vartheta_0 sin~\alpha = gt_{под}$
3. Высоту  подъёма можно  вычислить по  четырём формулам:

$h = \text{<}\vartheta_Y\text{>} t_{под}$

$h = \dfrac{\vartheta_{OY} + \vartheta_{AY}}{2}t_{под} = \dfrac{\vartheta_0 sin ~ \alpha}{2}t_{под}$

$h = \vartheta_{OY}t_{под} - \dfrac{gt_{под}^2}{2} = \vartheta_0 sin ~ \alpha t_{под} - \dfrac{gt_{под}^2}{2}$

$h = \dfrac{\vartheta_{AY}^2 + \vartheta_{OY}^2}{2g} = \dfrac{\vartheta_0^2 sin^2 ~ \alpha}{2g}$

$h = \vartheta_{AY}t_{пад} + \dfrac{gt_{пад}^2}{2} = \dfrac{gt_{пад}^2}{2}$

При этом надо помнить, что при свободном движении время подъёма равно времени падения $t_{под}=t_{пад}$, а все время движения можно найти по формуле $t_{всё}=2t_{пад}$

Рассмотрим теперь это движение в проекции на ось OX (движение вдоль оси Oх). Это движение  соответствует  равномерному  горизонтальному  движению (при  условии,  что нет  никаких  помех  со  стороны  других  тел по горизонтальному направлению):
OX:  По  определению  путь  тела  или  его  горизонтальное  перемещение равны  произведению  горизонтальной  проекции  скорости  на  время  горизонтального  движения: $S=\vartheta_{OX} t_{всё} = \vartheta_0 cos~\alpha t_{всё}$, т.е. $S=\vartheta_0cos~\alpha t_{всё}$

Если учесть, что $t_{всё}=2t_{под}$ и $t_{под}=\dfrac{\vartheta_0 sin~\alpha}{g}$,  тогда  формула дальности  полёта  примет  вид:
$S = \vartheta_0cos~\alpha~2t_{под} = \vartheta_0 cos ~\alpha~2\dfrac{\vartheta_0 sin~\alpha}{g} = \dfrac{\vartheta_0^2sin~2\alpha}{g}\text{, т.е. }S = \dfrac{\vartheta_0^2 sin~2\alpha}{g}$

Тогда,  зная  значение  высоты  подъёма  и  дальности  полёта,  можно  сравнить  эти  две  характеристики между  собой:
$!!! \dfrac{S}{h} = \dfrac{\vartheta_0 cos~\alpha\cdot 2\vartheta_0 sin~\alpha}{g} \dfrac{2g}{\vartheta_0^2 sin^2\alpha} = 4 ctg~\alpha $, т. е. дальность полёта $S$ в   $4ctg ~\alpha$ больше высоты подъёма $h$: 

$!!!~S > h\text{  в  }4ctg~\alpha$ Т.к. движение вдоль оси OX равномерное (на тело вдоль оси ОХ нет действия сил),  то скорость в любой точке на этой оси одинакова, т.е. все проекции скорости в  точках О, С, А  равны между собой
$\vartheta_{OX} = \vartheta_{CX} = \vartheta_{AX} = \vartheta_{BX} = \vartheta_{DX}$, где $\vartheta_{OX} = \vartheta_0 cos~\alpha$, $\vartheta_{CX} = \vartheta_C cos~\beta$, $\vartheta_{AX} = \vartheta_A$, $\vartheta_{BX} = \vartheta_B cos~\beta$, $\vartheta_{DX} = \vartheta_D cos~\alpha$

На  рисунке  видно,  что  проекции  скоростей( на  обе  оси  соответственно)  в  симметричных  точках  равны, но  отличаются  направлением.             
$\vartheta_0 cos~\alpha = \vartheta_C cos~\beta = \vartheta_A$ (проекция скорости на ось OX в т. А равна сама себе)

т.к.  это РМДв, то $\vartheta_{OX} = \vartheta_0 cos~\alpha = \vartheta_{DX} = \vartheta_D cos~\alpha$ (но начальная скорость подъёма, равна конечной скорости падения $\vec\vartheta_0~↑=↓ \vec\vartheta_D$). Угол между направлениями начальной и конечной скорости этого движения равен $2\alpha$.
Рассмотрим   первый  частный случай  этого  движения, когда  тело  бросают  горизонтально  с  некоторой  высоты:
Особенность  этого  случая  в  том  что  здесь   всё  время  движения  равно  времени  падения  тела: $t_{всё}=t_{пад}$  

Рассмотрим   второй   частный случай  этого  движения, когда  тело  бросают  под  углом    к  горизонту  или    вниз   или    вверх с  некоторой  высоты:

Такое  движение аналогично  первому  частному  случаю, но  при  этом $OY: \vartheta_{OY} = -\vartheta_0 sin~\alpha$ $h = -\vartheta sin~\alpha t_{под} - \dfrac{gt_{пад}^2}{2}$ $OX: \vartheta_{OX} = \vartheta_0 cos~\alpha$ $S = \vartheta_0 cos~\alpha t_{всё}$ $t_{всё}=t_{пад}$	Такое движение делится на два случая на движение под углом к горизонту (промежуток ОД) и случаю рассмотренному слева (промежуток ДМ), а значит используются соответствующие формулы.

При рассмотрении движения под углом необходимо помнить ещё одну  ОСОБЕННОСТЬ этого движения - это  движение  является симметричным  относительно  оси, проходящей  через  высоту подъёма, а  это  позволяет  сделать  следующий  вывод:
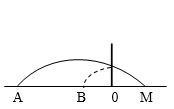
Если  на  пути  тела  «стоит» стена, от  которой  тело  при  упругом  ударе  отскочит, то расстояние, на  которое   оно  отлетит,    будет  равно  расстоянию  «непройденному» телом по  причине  «помехи»:

$AM (S)$ - дальность  возможного полёта,  если бы  не  было  стены. $AO (S_0)$ -  расстояние от тела до стены. $OB (S_1)$ - расстояние на  которое тело  отлетит после удара о  стену. $S = S_0+ S_1$,     $S_0 = S - S_1$,     $S_1 = S - S_0$

При  решении  такого  типа  задач  следут  найти   значение  возможной дальности  полёта $S$ (для случая без препятствия $S = \dfrac{\vartheta_0^2 sin~2\alpha}{g}$). Зная, на каком расстоянии находилось тело от стены, можно определить где оно окажется после удара.

Вернуться к конспектам урока