Движение  по  окружности  – частный случай криволинейного движения. 
При движении по окружности движение может быть:

1. С постоянной по величине скоростью $\vartheta = const$
2. С одинаково изменяющейся по величине  скоростью $\Delta \vartheta = const$
3. С неодинаково изменяющейся по величине скоростью, $\Delta \vartheta$ разное, изменяется не одинаково.

!!! Но при этом во всех 3-х случаях $\vartheta$ изменяется по направлению (всегда). Движение по окружности – это периодически  повторяющееся движение.
Основными  характеристиками  такого  движения  являются:
$T = \dfrac{t}{N}$ - период – это время 1 полного оборота ($t$ – все время, $N$ – число оборотов за время $t$)
$n=\dfrac{1}{T}=\dfrac{N}{t}$ - частота – число оборотов за 1с. (Гц)
$l = 2\pi R$ – путь за 1 поворот (длина окружности) (м)
$L = 2\pi RN$ – путь за $N$ оборотов (м).

1.Рассмотрим  движение  с  постоянной  по  величине  скоростью.

По  определению, скорость это путь, пройденнфй телом за единицу времени:
$\vartheta=\dfrac{L}{t}$ -  это путевая  скорость  движения  тела  по  окружности. Зная  значения величин, входящих  в  эту  формулу, получим формулы  скорости, которые выражают  зависимость  от  основных  характеристик  движения  по  окружности:

$\vartheta=\dfrac{2 \pi RN}{t} = 2 \pi Rn= \dfrac{2 \pi R}{T} = R \omega = \sqrt{a_ц R}$ $\omega = 2 \pi n$ – циклическая частота или угловая скорость (число оборотов за $2 \pi$ секунды), измеряется  в  (Гц = рад/с).
$\omega = \dfrac{2 \pi}{T}$ 
Аналогия: тело со $\vartheta$ тело проходит путь $L$, со  скоростью $\omega$ проходит угловой путь $\varphi$ (поворачивается  на  угол).
Угловое расстояние: $\varphi = \omega t$ или $\varphi = 2 \pi N$
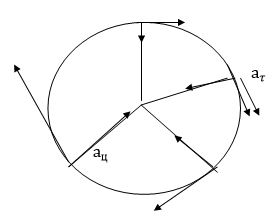
$a_ц = \dfrac{\vartheta^2}{R}$ - ускорение,  которое показываем изменение направления скорости (но не величины) т.к. $a_ц = \dfrac{\vartheta^2}{R}$ всегда  перпендикулярна $\vartheta$ и направлена к центру окружности, то это ускорение называется центростремительным:
$a_ц = \dfrac{\vartheta^2}{R}$ - формула, определяющая центростремительное  ускорение. Подставляя вместо скорости её формулы, получим расчётные формулы для центростремительного ускорения: $a_ц=4 \pi^2 n^2R=\omega^2 R=\dfrac{4 \pi^2 R}{T^2}=\vartheta \omega$ формулы для  вычисления  центростремительного  ускорения  через  основные  характеристики.
Рассмотрим  частные  случаи  движения  тел  по  окружности:
1. Движение  по  одному  кругу, но  по  окружностям  разного  радиуса:
           

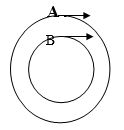
Если т.А и т.В двигаются синхронно то они вместе совершают 1 оборот,  значит $T_1=T_2$ (периоды их оборотов одинаковы), а из этого следует
$\Rightarrow n_1=n_2 \Rightarrow \omega_1 = \omega_2$   
Зная  связь   между  линейной  и  угловой  скоростями, между  ускорением   и угловой  скоростью, получим  выражения:
$\dfrac{\vartheta_1}{R_1}=\dfrac{\vartheta_2}{R_2}\Rightarrow \dfrac{\vartheta_1}{\vartheta_2}=\frac{R_1}{R_2}$
$\sqrt{\dfrac{a_1}{R_1}} = \sqrt{\dfrac{a_2}{R_2}} \Rightarrow \dfrac{a_1}{R_1} = \dfrac{a_2}{R_2} \Rightarrow \dfrac{R_1}{R_2}=\dfrac{a_1}{a_2}$
2. Рассмотрим  случай, когда   два  тела  совершают  круговые  движения,  но  связаны   ременной  или  зубчатой  передачей

  ременная связь или зубчатая связь
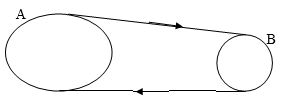
В этом  случае скорости  движения  двух  тел  равны (нет  провисания  ремня): $\vartheta_1=\vartheta_2$
 Зная  формулы, связывающие  линейную  скорость  с  периодом  вращения  и   с  ускорением,   получим: 
$\dfrac{R_1}{T_1}=\dfrac{R_2}{T_2} \Rightarrow \dfrac{R_1}{R_2}=\dfrac{T_1}{T_2}$
$\dfrac{R_1}{R_2}=\dfrac{n_2}{n_1}$
$\dfrac{R_1}{R_2}=\dfrac{a_2}{a_1}$   
2. Более  сложный  случай,  когда  скорость  изменяется  по  величине.
$\left \langle \vartheta \right \rangle = \dfrac{L}{t}$  -   это средняя   путевая  скорость  движения  тела  по  окружности, где её  изменение  по  величине  характеризуется  тангенциальным  ускорением: $a_{\tau}$,   изменение  скорости  по  направлению  характеризуется  центростремительным  ускорением $a_ц$, которое  в  каждой  точке  разное,  так  как  разной  будет  скорость  движения  по  величине: $a_ц = \dfrac{\vartheta^2}{R}$.  Эти  два  ускорения  взаимно  перпендикулярны  т.к. $a_ц$ направлено  к  центру  окружности,  а  $a_{\tau}$ - по  касательной (если разгон, то  по  направлению  скорости,  если  торможение, то  в  противоположную  сторону).

Так  как  тангенциальное  ускорение  не  изменяется, а  центростремительное  изменяется,  то  будет    изменяться   и  общее  ускорение  $a=\sqrt{a_ц^2+a_{\tau}^2}$
Изменение  скорости приведёт  к  изменению  связанных  с  ним  характеристик: периода, частоты  и   угловой  скорости  вращения.

Вернуться к конспектам урока