$\vec p = m \vec\vartheta$ - произведение массы тела на его скорость – это импульс тела.
Пусть на тело действует сила $\vec F$, если она не равна 0, то она заставляет тело двигаться с ускорением (из кинематики $\vec a = \dfrac{\vec\vartheta - \vec\vartheta_0}{t}$). Согласно 2 закону Ньютона получим: $F = ma$
Если вместо ускорения подставить его формулу и обе части уравнения умножить на промежуток времени, то получим следующее уравнение $\vec F t = m\vec\vartheta - m\vec\vartheta_0$. В этом уравнении величина слева $Ft$ называется импульсом силы, а величина справа показывает изменение импульса тела под действием импульса силы. Величина $m\vartheta_0$ называется начальным импульсом тела (импульс тела в момент времени $t_0$), величина $m\vartheta$ называется конечным импульсом тела (импульс тела в момент времени $t$). Величина $m\vartheta - m\vartheta_0$ называется изменением импульса тела или разность конечного и начального импульса тела.

Т.к. обе части уравнения равны, то делаем вывод: импульс силы равен изменению импульса тела.
т.е. $F$ это причина изменения импульса тела.
Вспомним III закон Ньютона: если 2 тела взаимодействуют, то силы с которыми они действуют друг на друга равны, но направлены в противоположные стороны. Если каждая сила вызывает движение тел с ускорением, то после преобразования получим:

$\vec F_1 = - \vec F_2$
$m_1 \vec a_1 = - m_2 \vec a_2$
$m_1 \dfrac{\vec\vartheta_1 - \vec\vartheta_{01}}{t} = - m_2 \dfrac{\vec\vartheta_2 - \vec\vartheta_{02}}{t}/ \cdot t$
$m_1 \vec\vartheta_1 - m_1\vec\vartheta_{01} = - (m_2 \vec\vartheta_2 - m_1\vec\vartheta_{02})$

Слева $\Delta m_1 \vec\vartheta_1$ изменение импульса первого тела.           
Справа $\Delta m_2 \vec\vartheta_2$изменение импульса второго тела.
Тогда из полученной конечной формулы сделаем 1 вывод: $\Delta \vec p_1 = - \Delta \vec p_2$ если тела взаимодействуют, то их импульсы меняются на одинаковую величину. Знак «-» говорит, что импульс тел изменяется по-разному если один увеличивается , то второй на столько же уменьшается.
2 вывод: перенесем начальные и конечные импульсы тел в разные стороны. Слева соберём все начальные импульсы, справа все конечные $m_1 \vec\vartheta_{01} + m_2 \vec\vartheta_{02} = m_1 \vec\vartheta_1 + m_2 \vec\vartheta_2$. Получаем уравнение, которое называется законом сохранения импульса тел:
!!! сколько бы тел ни взаимодействовало: геометрическая $\Sigma$ импульсов всех тел до взаимодействия = геометрической $\Sigma$ импульсов тел после взаимодействия.

При решении задач на закон сохранения импульса необходимо использовать аналогичное правило правилу решения задач на Динамику:

1) после внимательного прочтения условия задачи делаем рисунок с указанием всех векторов скорости всех тел;

2) записываем закон сохранения импульса в векторной форме;

3) выбираем направление осей координат ОХ и, если нужно, ОУ, затем находим проекции импульсов на эти оси и записываем закон сохранения импульсов тел в проекции;

4) выражаем нужную для нахождения величину (при этом, если нужно, заменяем массу тела или скорость тела их формулами $m = V\cdot\rho = N\cdot m_0$, $\vartheta = \dfrac{l}{t}$);

5) делаем подстановку значений, вычисляем и получаем ответ.

Поведение движущихся и взаимодействующих тел обладает некоторыми особенностями:

а) Если два тела движутся навстречу друг другу, так что их центры находятся на одной линии, и имеют одинаковые массы и размеры, то после удара, который является центральным, они обменяются скоростями (значениями и направлениями):

до столкновения,

после столкновения.

Скорость первого тела стала после удара скоростью второго тела и наоборот. !!! Но это выполняется только для одинаковых тел и если удар центральный.

б) Если тела одинаковых масс, но удар нецентральный (боковой), то после столкновения тела разлетятся под прямым углом (90⁰ ).

до взаимодействия,

после столкновения.

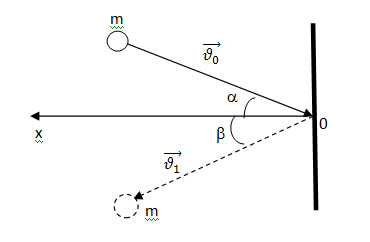
в) рассмотрим удар тела о неподвижную опору:

В соответствии с законом отражения угол падения тела на стену $\alpha$ равен углу отражения $\beta$ (отскока) от стены. Если удар упругий, то скорость падения по величине равна скорости отскока тела после удара, в этом случае сохраняется и энергия удара (нет потерь).

В этом случае импульс силы удара в проекции на ось ОХ ( направление оси выбирается по напавлению конечного импулься и часто перпендикулярно стене): $Ft = m\vartheta_1 cos~\beta - (-m\vartheta_0 cos~\alpha) = 2m\vartheta cos~\alpha$. Если удар будет проходить вдоль перпендикуляра, то ответ будет
$Ft = m\vartheta_1 - (-m\vartheta_0) = 2m\vartheta$. Если же есть потери энергии (или массы, или скорости), то формула примет вид
$Ft = Xm\vartheta_1 - (-m\vartheta_0) = m\vartheta (X + 1)$, где $X$ будет долей оставшейся после потерь (например если потери составили 30%, то $X=0.7$ части от начальной скорости или массы).

Вернуться к конспектам урока