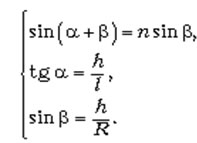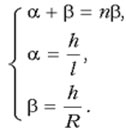Рассмотрим поведение световых лучей, падающих на одну из граней призмы.

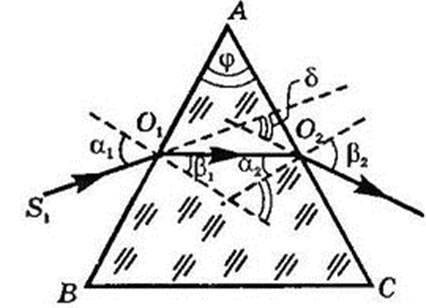
Пусть монохроматический свет падает на грань АВ стеклянной призмы (на границу раздела воздух-стекло), находящейся в воздухе; S₁O₁ - падающий луч; - угол падения из воздуха в стекло, O₁O₂ - преломлённый луч после перехода из воздуха в стекло; - угол преломления. Так как свет переходит из воздуха (из среды оптически менее плотной) в стекло (в среду оптически более плотную), то Пройдя через призму луч падает на вторую грань АС. Здесь он снова преломляется, но уже на границе стекло-воздух: О₁О₂ - падающий луч на границу стекло-воздух;

S₂ - преломлённый луч, вышедший из точки О₂; - угол падения из стекла в воздух; - угол преломления. Так как свет здесь переходит из стекла (из среды оптически более плотной) в воздух (в среду оптически менее плотную), тоГрани ВА и АС, на которых происходит преломление света, называются преломляющими гранями. Угол между преломляющими гранями называется преломляющим углом призмы. Угол , образованный направлением луча, входящего в призму , и направлением луча, выходящего из неё, называют углом отклонения. Грань ВС, лежащая против преломляющего угла, называется основанием призмы.

Для первой преломляющей грани ВА закон преломления записывается так: , где n_ст - абсолютный показатель преломления стекла (так как призма находится в воздухе).

Для второй преломляющей грани АС закон преломления записывается Преломляющий угол призмы можно найти по формуле, а угол отклонения.

Как видно из рисунка, если луч падает из менее оптически плотной среды в более плотную, то после прохождения призмы, вышедший луч отклоняется к основанию призмы. Несложно догадаться, что если луч упадёт на призму из оптически более плотной среды в менее плотную, то после прохождения призмы, световой луч отклонится к её вершине.

Примеры:

1. Луч света падает на переднюю грань трёхгранной призмы с преломляющим углом, которая находится в воздухе. После преломления он падает на заднюю грань призмы и выходит в воздух. Определите угол отклонения светового луча, если угол падения на переднюю грань равен, а абсолютный показатель преломления вещества призмы n.

Решение: Изобразим ход луча в призме.

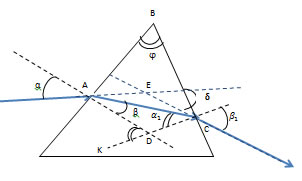
Как внешний угол к треугольнику АЕС, угол отклонения равен: (1). Кроме того углы АВС и ADK равны между собой и равны, как углы образованные взаимно перпендикулярными сторонами. Угол ADK является внешним углом к треугольнику ADС, поэтому (2). Из уравнений (1) и (2) получим:

(3).Согласно закону преломления (4)

Выразив из уравнения (2) и подставив его значение в уравнение (4) получим: (5). Из уравнеия (4) выразим , найдём:

и подставим их формулы в уравнение (5) и получим:

(6). С учёто уравнений (3) и (6) получим выражение для угла :

. Это и есть ответ на вопрос задачи.

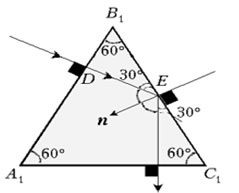
2. Поперечное сечение стеклянной призмы имеет форму равностороннего треугольника. Луч света падает из воздуха на одну из граней призмы перпендикулярно ей. Найти угол между лучом, выходящим из призмы, и продолжением луча, падающего на призму. Показатель преломления стекла n = 1,5. 

Решение: Угол при вершине призмы равен 60° (сечение призмы – равносторонний треугольник). Первую грань луч пройдёт не преломляясь (угол падения на грань равен нулю, следовательно, и угол преломления равен нулю). На вторую грань луч упадёт тоже под углом 60°к поверхности (смотри рисунок). Как видно из рисунка луч падает на первую грань призмы по нормали к ней, то в точке D он не преломляется и прямолинейно доходит до точки E.

 

Запишем для этой точки (Е) закон преломления:, распишем углы и получим откуда , чего не может быть. Следовательно, в точке E будет полное внутреннее отражение, и через вторую грань луч из призмы не выйдет. Геометрически ясно, что, отразившись от второй грани, луч пойдёт по нормали к третьей. А значит, он выйдет из призмы без преломления. Таким образом, искомый угол при вершине Е: 2 • 60° = 120°. Ответ:120°

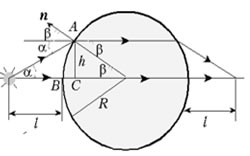
3.Стеклянный шар (показатель преломления n) освещается узким расходящимся пучком лучей, ось которого проходит через центр шара. Источник света расположен на расстоянии l от поверхности. На таком же расстоянии от поверхности, но по другую сторону от шара, находится изображение источника. Определите радиус шара.

Решение. Изображение источника света находится, очевидно, в точке пересечения любого луча пучка и осевого луча.

Главное – сообразить, что в силу симметрии источника света и его изображения относительно центра шара и обратимости световых лучей, луч внутри шара пойдёт горизонтально. Чтобы не загромождать выкладки, сразу пренебрегаем длиной отрезка BC по сравнению с радиусом шара. По закону преломления света в точке A и из очевидных на рисунке треугольников, имеем систему уравнений:

При замене синуса и тангенса малых углов самими углами система радикально упрощается:

Подставляя из второго и третьего уравнений углы  и  в первое уравнение, придём к результату: R = l(n – 1). Ответ: R = l(n – 1)

Вернуться к конспектам урока